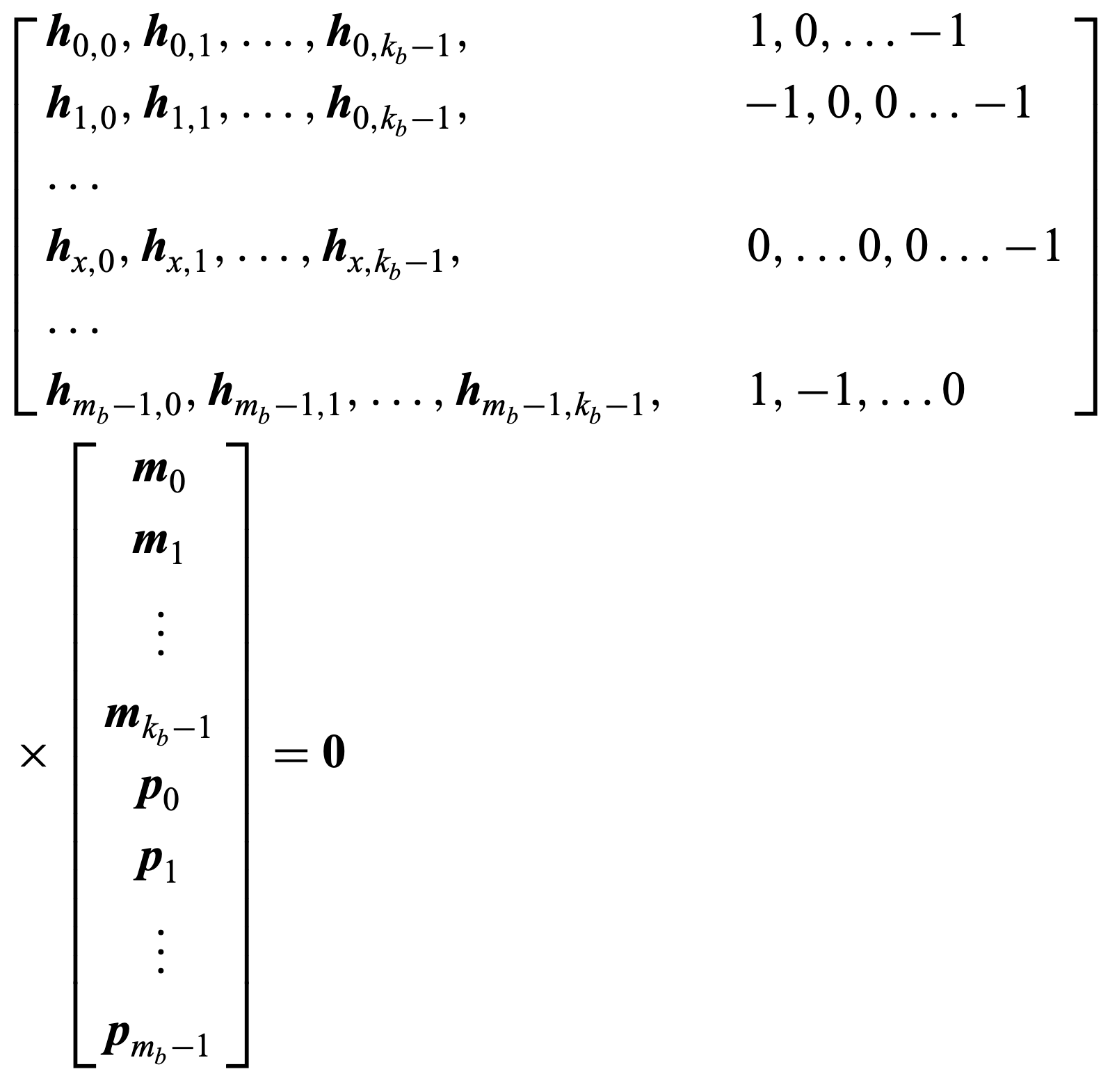
The described algorithm is taken from Efficient encoding of IEEE 802.11n LDPC codes. The form of the parity check matrices enables an efficient encoding scheme. Consider the parity check matrix shown before in block form:

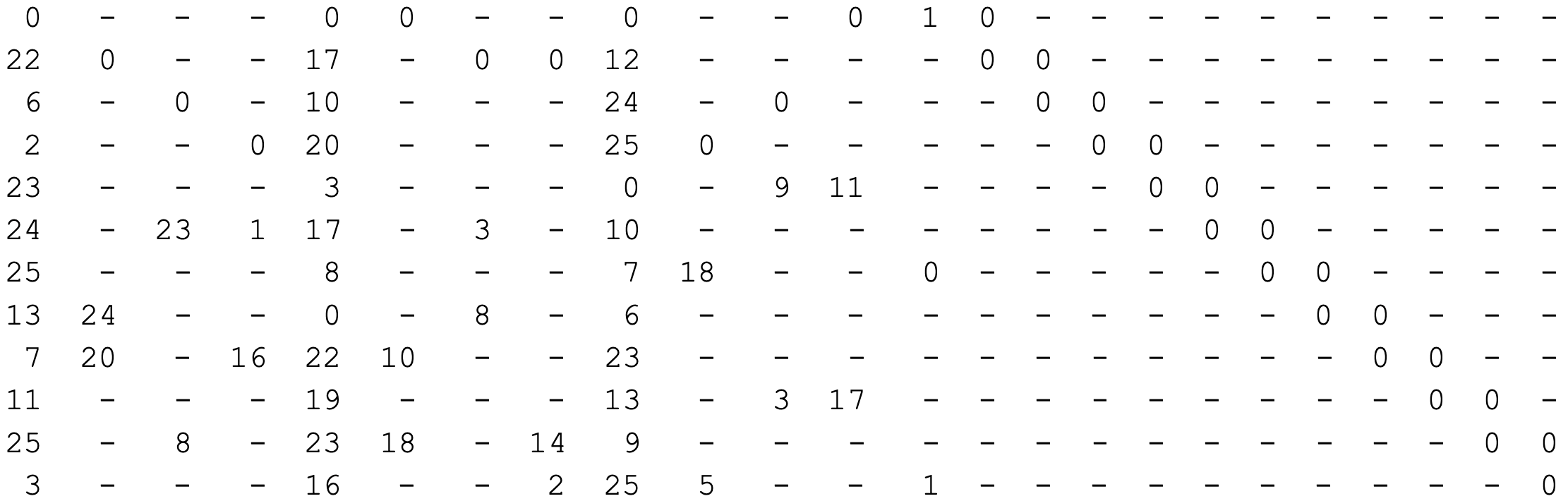
Parity check matrix for $n=648$ bits and rate $r=1/2$, taken from IEEE802.11-2020 Standard

Above, dashes indicate all zero sub-blocks, and numbers indicate the number of shifts per sub-block. Values of $0$ indicate identity matrices. The observed format of double diagonal on the far right is shared among all codes in the standard and enables efficient encoding. Specifically, all the matrices for codes in the standard share the following structure. For a block matrix of dimensions $m_b\times n_b$, there are varying structures for the first $k_b$ columns. However, the $k_b$-th column always has exactly three non-zero blocks, two blocks labeled as $1$ in the top and bottom row, and one identity row labeled as the $x$-th row. To the right of the $k_b$-th column, there are $m_{b}-1$ columns which exhibit the shown double diagonal form.

Let us denote the input information sequence as $m$ and divide it into $k_b= n_b-m_b$ groups of $Z$ bits, i.e. $m=[m_0, m_1, \dots, m_{k_b-1}]$, where each element of $m$ is itself a vector of length $Z$. The parity sequence can also be grouped as length of $Z$ bits and expressed as: $p=[p_0, p_1, \dots, p_{m_b-1}]$. correspondingly, codewords may be expressed as:

\[c=[m, p]=[m_0, m_1, \dots, m_{k_b-1},p_0, p_1, \dots, p_{m_b-1}]\]

Since every valid codeword must adhere to $Hc^T=0$, we may expand this equation as:

Taken from Efficient encoding of IEEE 802.11n LDPC codes

These equations may be divided into a set of four types of equations; The top, bottom, and $x$-th row are unique, and an equation for all other rows. These are expressed as:

\[\begin{align} &\sum_{j=0}^{k_b-1} h_{0,j}m_j + \Pi_1p_0+ p_1=0,\;\;\;\;(0th\; row)\\ &\sum_{j=0}^{k_b-1} h_{i,j}m_j + p_i + p_{i+1}=0,\;\;\;\;(i\neq 0,x,m_b-1)\\ &\sum_{j=0}^{k_b-1} h_{x,j}m_j + p_0 + p_x + p_{x+1}=0,\;\;\;\;(xth\; row)\\ &\sum_{j=0}^{k_b-1} h_{m_b-1,j}m_j + \Pi_1p_0+ p_{m_b-1}=0,\;\;\;\;(m_b-1\; row)\\ \end{align}\]

where $\Pi_1$ is the identity matrix shifter one column to the right. In the above, all equalities are interpreted as summation modulo 2. To simplify the above equations, we sum them to obtain:

\[p_0=\sum_{i=0}^{m_b-1} \sum_{j=0}^{k_b-1} h_{i,j}m_j = \sum_{i=0}^{m_b-1}\lambda_i = 0\]

with $\lambda_i= \sum_{j=0}^{k_b-1} h_{i,j}m_j$. With $p_0$ in hand and using top and bottom equations:

\[\begin{align} &p_1=\lambda_0+\Pi_1p_0\\ &p_{m_b-1}=\lambda_{m_b-1} + \Pi_1p_0 \end{align}\]

Using equations for the $i$-th and $x$-th row, all other parity bits can be found recursively. The procedure can even be made simpler! Due to the form of the matrices $h_{i,j}$, the multiplications $h_{i,j}m_j$ reduce circular shifts of the vectors $m_j$! Thus, encoding reduces to a summation of circular shifts of message bits. Moreover, to avoid recomputing $\lambda_i$, given a message sequence, all $m_b$ $\lambda_i$’s may be computed and stored in memory (each of them is a vector of $Z$ bits). The recursive algorithm then needs only to sum them once to obtain $p_0$ and then use each of them once more during the computation.

This algorithm has been implemented in the repo.